Contents

1 ¿Qué es una señal?

• Una señal es cualquier perturbación física medible que transporta información.
  1. Una señal de audio afecta a la presión que el aire ejerce sobre la membrana de un micrófono. Una señal de audio puede medirse como el desplazamiento que sufre la membrana respecto de su posición de equilibro.
  2. En el caso de una imagen, una señal luminosa afecta al tipo y cantidad de radiación electromagnética que alcanza un dispositivo sensible a la luz, como puede ser una película fotográfica.
• En general, una señal expresa variaciones continuas de una magnitud física y se habla, en este caso, de señal analógica.

2 ¿Qué se obtiene tras muestrear una señal?

• La naturaleza analógica de las señales hace imposible su manipulación mediante sistemas digitales. Por este motivo previamente se digitalizan.
• El muestreo es la primera etapa que se realiza cuando digitalizamos señales [7].
  1. Una señal de audio muestreada es igual a la señal de audio original en aquellos puntos donde se toma cada muestra.
  2. En el caso de una imagen estática (la que tomamos con una cámara de fotos), el muestreo produce una matriz bidimensional de muestras recogidas en diferentes puntos espaciales.
  3. Para una señal de vídeo muestreamos tanto en el dominio del espacio como en el del tiempo. Así lo que obtendríamos sería una secuencia de imágenes como las del caso anterior.

3 El Teorema del Muestreo (Uniforme) de Nyquist-Shannon

• Sea $s\left(t\right)$ una señal limitada en banda, que no tiene componentes espectrales mayores que la frecuencia $f_m$ Hz. El Teorema del Muestreo Uniforme indica que $s\left(t\right)$ queda determinada de forma única (sin pérdida de información) por sus valores a intervalos uniformes de tiempo menores o iguales que $\frac{1}{2f_m}$ segundos [6]. Es decir, la frecuencia de muestreo $f_s$ debe de ser

  $$f_s\ge 2f_m.$$

• A la frecuencia $2f_m$ se le conoce como frecuencia de muestreo de Nyquist.

Demostración

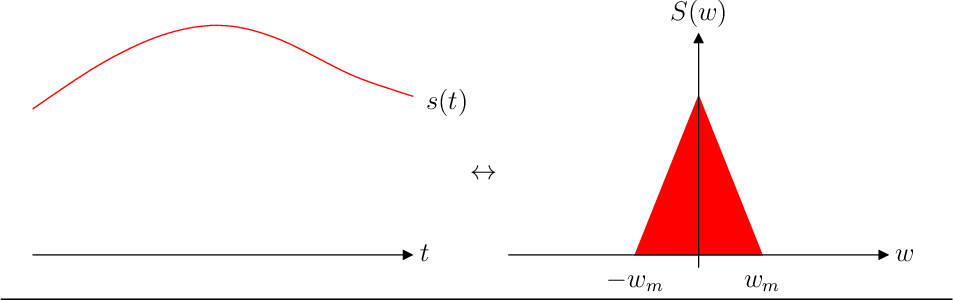
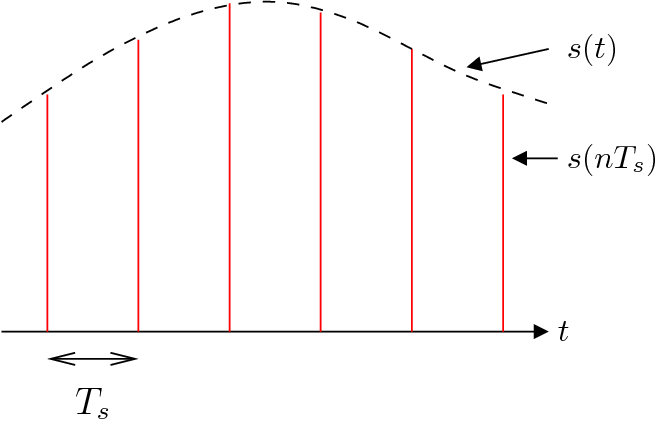
Según el enunciado se tiene que $S\left(w\right)=0$ cuando $\left|w\right|>w_m$ (está limitada en banda), donde $w_m=2\pi f_m$ sería la máxima componente de frecuencia angular de $s\left(t\right)$. Gráficamente:

El proceso de muestreo se modela matemáticamente mediante la multiplicación de $s\left(t\right)$ con un tren de impulsos unitarios ${\delta }_{T_s}\left(t\right)$ de periodo $T_s$. Sea

la señal resultante de dicho producto, donde (véase (${\delta }_T\left(t\right)$))

y

es el periodo de muestreo, siendo

la frecuencia de muestreo angular expresada en radianes/segundo. Como ya hemos demostrado (véase $\mathcal{ℱ}\left[{\delta }_T\left(t\right)\right]$),

Teniendo en cuenta que la multiplicación de dos funciones en el dominio del tiempo equivale a la convolución de sus espectros (Eq. ConvF), se tiene que

Al substituir $w_s=\frac{2\pi }{T_s}$, obtenemos que

que por definición de ${\delta }_{w_s}\left(w\right)$ (ver de nuevo la Eq. $\mathcal{ℱ}\left[{\delta }_T\left(t\right)\right]$) es

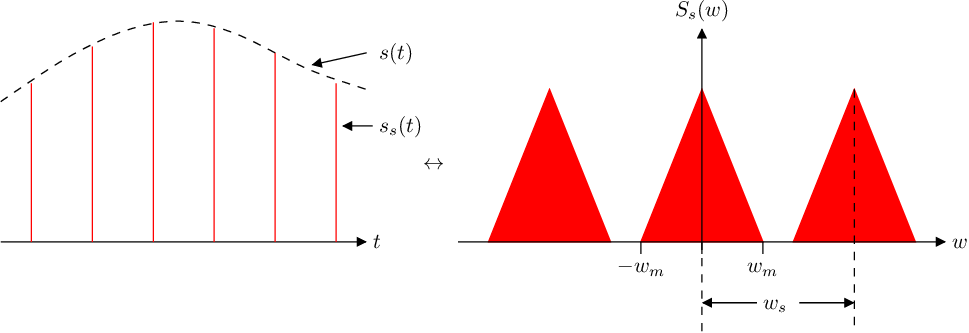
Por tanto, el espectro de una señal muestreada es igual a la replicación cada $w_s$ radianes/segundo del espectro de la señal original. Gráficamente:

Como se puede deducir de la representación gráfica de $S_s\left(w\right)$, podemos recuperar $s\left(t\right)$ a partir de $s_s\left(t\right)$ si filtramos las componentes de frecuencia superiores a $w_m$. Esto puede hacerse si multiplicamos $S_s\left(w\right)$ (en el dominio de la frecuencia, claro) por una función pulso rectangular

Esta función es en realidad la función de transferencia¹ de un filtro paso bajo con frecuencia de corte $w_m$ y ganancia $T_s$.

El Teorema del Muestreo Uniforme indica que para que la señal $s\left(t\right)$ sea recuperable a partir de la señal $s_s\left(t\right)$ debe cumplirse que

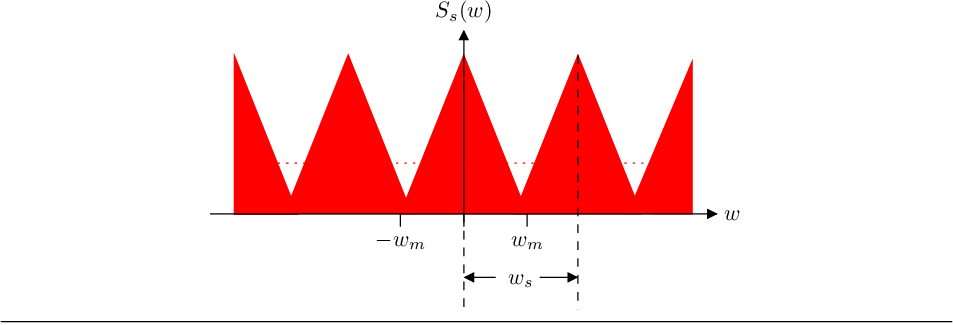
La demostración de esto en virtud de los resultados obtenidos es muy sencilla. En el caso de que $w_s<2w_m$ entonces sería imposible aislar el espectro de $s_s\left(t\right)$ mediante el filtro paso bajo y por tanto, no podríamos reconstruir $s\left(t\right)$ porque los espectros vecinos de $s\left(t\right)$ se solaparían. Gráficamente:

En esta situación sería imposible aislar el espectro de $s\left(t\right)$ a partir de $s_s\left(t\right)$ mediante la aplicación de un filtro paso bajo de frecuencia de corte $w_s$.

4 Ninguna señal finita está limitada en banda

• Las señales finitas son aquellas que sólo están definidas durante un intervalo de tiempo finito. Fuera del mismo se considera que valen cero.
• Según la teoría matemática de Fourier, es posible encontrar una representación para una señal finita que utiliza un número infinito de coeficientes de frecuencia (Eq. stf).
• Como los coefcientes de Fourier se especifican en frecuencias múltiplos de la frecuencia fundamental $w_0$ (el espectro es discreto) [5] y existen infinitos coeficientes, necesariamente se ocupa un ancho de banda infinito.
• Este hecho también puede determinarse si nos fijamos en el proceso que sería necesario si queremos obtener una señal finita a partir de una infinita $s\left(t\right)$ (que podría estar limitada en banda o no):

  Multiplicar la señal $s\left(t\right)$ infinita y limitada en banda por una función rectangular $g_{\tau }\left(t\right)$, en el dominio del tiempo.

  Como sabemos, multiplicar dos señales en el dominio del tiempo equivale a convolucionar sus espectros. Como el espectro de una función cuadrada no es igual a una función impulso unitario (excepto en el caso de que la duración de la función $\tau =\infty$, véase la Sección La transformada de Fourier de una función rectangular), el espectro de la función que realmente estamos muestreando no es igual al espectro de $s\left(t\right)$ y por supuesto, no está limitado en banda puesto que $G_{\tau }\left(w\right)$ no lo está.

• Esto último provoca que sea imposible muestrear una señal durante un periodo finito de tiempo y luego reconstruirla sin pérdida de información, excepto en el caso de que sea periódica y de periodo $\tau$.

5 El muestreo de señales finitas (en el tiempo)

• Para eliminar el efecto de la deformación del espectro de una señal a causa de limitar su muestreo a un intervalo de tiempo finito, lo ideal sería utilizar una función ventana cuyo espectro fuera una función impulso unitario [8]. Para conseguir esto (por desgracia en la práctica sólo parcialmente) podemos hacer 2 cosas:
  1. Aumentar el tamaño de la ventana tanto como se pueda.
  2. Utilizar ventanas cuyo espectro se parezca lo máximo posible a una función impulso unitario (máxima acumulación de energía en un intervalo de frecuencias tan pequeño como sea posible). Así minizaremos lo que se conoce como el fenómeno de la dispersión espectral o leakage.

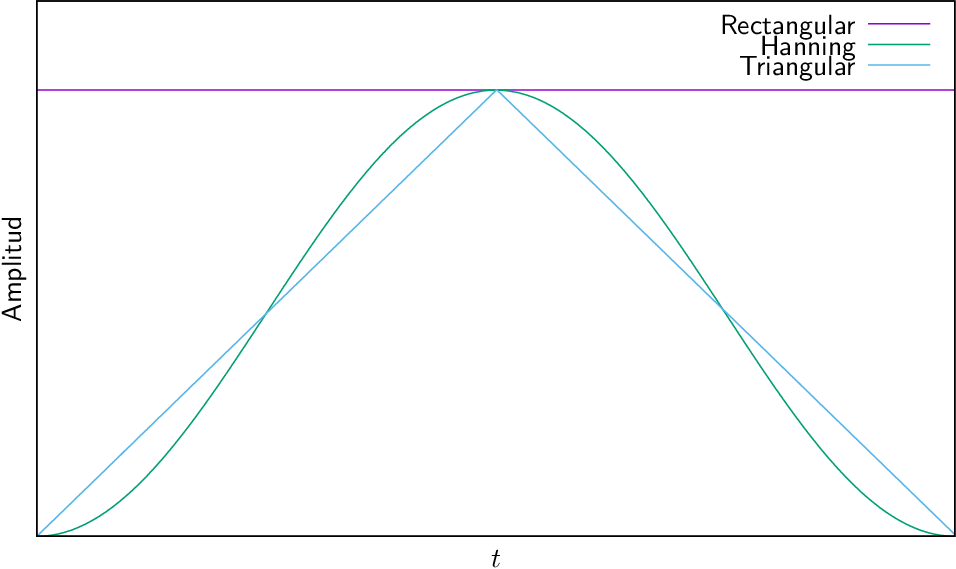
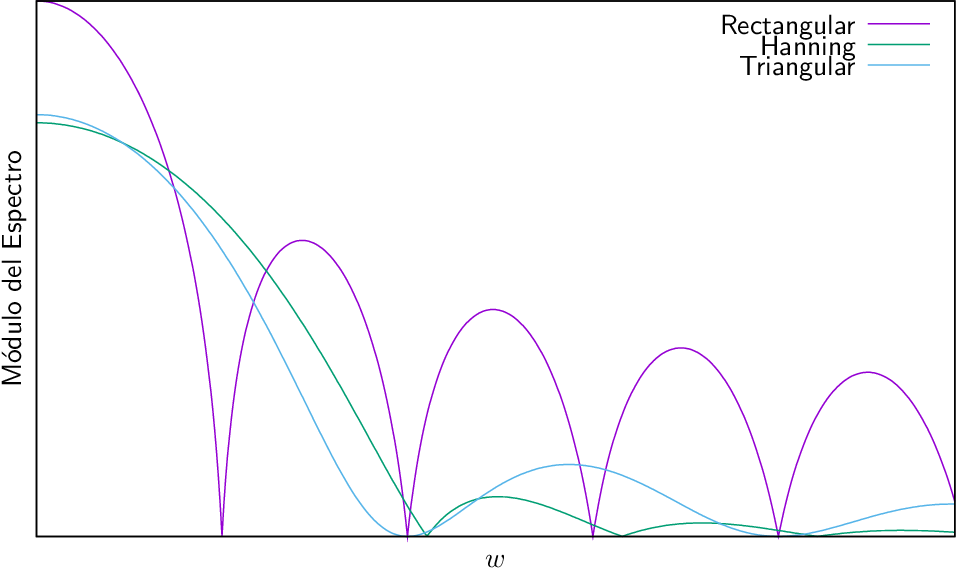
• Este hecho es importante de cara a representar los espectros y algunos investigadores ya han encontrado funciones ventana que tratan de hacer esto. Ejemplos de ventanas temporales son:
  1. Ventana rectangular:

     $$g_{\tau }\left(t\right)=\left\{\begin{array}{cc}1\hfill & \text{si }\left|t\right|<\frac{\tau }{2}\hfill \\ 0\hfill & \text{resto}\hfill \end{array}\right.$$

  2. Ventana de Hanning (von Hann):

     $${\text{Hanning}}_{\tau }\left(t\right)=\left\{\begin{array}{cc}0.5-0.5cos\left(2\pi t\right)\hfill & \text{si }\left|t\right|<\frac{\tau }{2}\hfill \\ 0\hfill & \text{resto}\hfill \end{array}\right.$$

  3. Ventana de Barlett (o triangular):

     $${\text{Barlett}}_{\tau }\left(t\right)=\left\{\begin{array}{cc}2t\hfill & \text{si }-\frac{\tau }{2}<t\le 0\hfill \\ -2t\hfill & \text{si }0<t\le \frac{\tau }{2}\hfill \\ 0\hfill & \text{resto}\hfill \end{array}\right.$$

6 El proceso de muestreo

• Un sampler de audio es un dispositivo con una entrada analógica, por la que entra la señal analógica de audio $s\left(t\right)$ y una salida analógica, por donde sale la señal analógica $s_s\left(t\right)$, que para enfatizar que se trata de una señal que sólo toma valores diferentes de cero en los instantes múltiplos del periodo de muestreo, en adelante la representaremos como

  $$s_s\left(t\right)=s\left(n{T}_s\right),$$

  (1)

  donde $n\in \mathcal{𝒵}$ [7].

  

• El número de muestras/segundo que obtenemos depende de la frecuencia de muestreo $f_s=1∕T_s$.
• Internamente, en general un sampler de audio tiene un filtro paso bajo para eliminar las frecuencias superiores a $f_s∕2$ y evitar así el solapamiento espectral (aliasing).

7 PAM (Pulse-Amplitude Modulation)

• Modulation: Samplers produce PAM signals $s\left(n{T}_s\right)$. Notice that a PAM signal usually represents an analog information source.

  

• Demodulation: To reconstruct $s\left(t\right)$ using $s\left(n{T}_s\right)$ it is neccesary to interpolate the signal using a low-pass filter with cutoff frequency $w_m$.

8 Muestreo en dos dimensiones (imágenes)

• Es una generalización del muestreo de audio al caso bidimensional (dimensiones X e Y). Por lo demás el proceso es el mismo. Un sampler para capturar imágenes muestrea a una determinada frecuencia (normalmente la misma) en ambas dimensiones y genera una matriz bidimensional para cada imagen.
• Notaremos a las muestras de una imagen como $$s\left(x{T}_{\text{X}},y{T}_{\text{Y}}\right);x\in \mathcal{𝒵},y\in \mathcal{𝒵},$$

  donde $T_{\text{X}}$ es el periodo de muestreo en el dominio X y $T_{\text{Y}}$ en el dominio Y.

9 Muestreo en tres dimensiones (vídeo)

• Es una generalización del muestreo de imágenes, donde se captura una imagen cada determinado intervalo de tiempo.
• La frecuencia de muestreo temporal (número de imágenes/segundo) debería permitir la sensación de movimiento. En la práctica bastan aproximadamente 25 imágenes/segundo, aunque este valor debería aumentar si la cantidad de movimiento es muy alta.
• Notaremos a las muestras de vídeo como $$s\left(x{T}_{\text{X}},y{T}_{\text{Y}},t{T}_{\text{T}}\right);x\in \mathcal{𝒵},y\in \mathcal{𝒵},t\in \mathcal{𝒵},$$

  donde $T_{\text{T}}$ es el periodo de muestreo temporal.

10 Algunos Casos Reales

• En un CD (Compact Disk) de audio, la frecuencia de muestreo es de $44.100$ muestras/segundo. Esto significa que la máxima componente de frecuencia representada es igual a $22.050$ Hz.
• En un SuperAudio CD, la frecuencia de muestreo es igual a $2.8224$ MHz.
• En el sistema Dolby Digital las frecuencias de muestreo son de $32$ kHz, $44.1$ kHz y $48$ kHz [1].
• En el sistema DTS (Digital Theather System) las frecuencias de muestreo son $32$ kHz, $44.1$ kHz, $48$ kHz y $192$ kHz [1].
• En el sistema PAL (Phase Alternating Line) el número de imágenes por segundo es igual a $25$. En el sistema NTSC (National Television System Committee) $30$. Nótese sin embargo que ambos representan las líneas de cada imagen de forma analógica ($625$ líneas en PAL y $512$ en NTSC).
• En MPEG-1 (Motion Picture Experts Group) [4] (Video CD), la resolución del vídeo tiene que ser inferior a $768\times 576$ puntos.
• En MPEG-2 [3] (DVD o Digital Versatile/Video Disk) la resolución tiene que ser inferior a $1920\times 1080$ puntos. Los DVD’s PAL almacenan típicamente imágenes de $720\times 576$ puntos (PAL DVDs) y los NTSC $720\times 480$ puntos [2].

References